第一章复习题第7题答案
证明：（1）如图1-5-26所示，
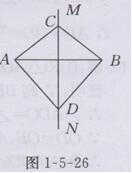
∵C是线段AB的垂直平分线上的点，
∴AC=BC.
∴△ABC是等腰三角形.同理可证△ABD是等腰三角形.
（2）第一种情况：点C，D在小段AB所在直线的异侧.
∵AC=BC,
∴∠CAB=∠CBA.
∵AD=BD,
∴∠DAB=∠DBA .
∴∠CAB+∠DAB=∠CBA+∠DBA,即∠CAD=∠CBD.
第二种情况：点C,D在线段AB所在直线的同侧，利用同样方法推理可得∠CAD=∠CBD.
第一章复习题第8题答案
已知：线段a（如图1-5-27所示）.求作：等腰△ABC，使得AB=AC，BC=a，BC边上的高AD=2a.
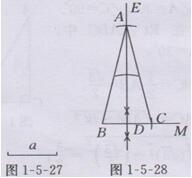
作法：如图1-5-28所示.（1）作射线BM，在BM上截取线段BC=a；（2）作线段BC的垂直平分线DE交BC于点D；（3）在射线DE上截取DA=2a；（4）连接AB,AC,则△ABC即为所求.
第一章复习题第9题答案
解：在Rt△ABC中，
∵∠BAC=90°，AB=AC=a，
∴BC=a.
∵AD⊥BC，
∴BD=1/2BC=/2a.
∵AD⊥BC，∠B=45°，
∴AD=BD=/2a.
第一章复习题第10题答案
解：①Rt△AOD≌Rt△AOE .
证明：
∵高BD，CE交于点O，
∴∠ADO=∠AEO=90°.
∵OD=OE，AO=AO,
∴Rt△AOD≌Rt△AOE（HL）.
②Rt△BOE≌Rt△COD.
证明：
由①知∠BEO=∠CDO=90°，
又∵OE=OD且∠BOE=∠COD,
∴△BOE≌△COD（ASA）.
③Rt△BCE≌Rt△CBD.
证明：
由②知∠BEC=∠CDB=90°，BE=CD且BC=CB,
∴Rt△BCE≌Rt△CBD（HL）.
④△ABM≌△ACM.
证明：
由③知∠ABC=∠ACB，由①知∠BAM=∠CAM,又
∵AM=AM，
∴△ABM≌△ACM（AAS）.
⑤Rt△ABD≌Rt△ACE.
证明：
∵∠ADB=∠AEC=90°，∠BAD=∠CAE，又由①知AE=AD,
∴△ABD≌Rt△ACE（ASA）.
⑥△BOM≌△COM.
证明：由①知∠AOE=∠AOD，由②知∠BOE=∠COD,
∴∠AOE+∠BOE=∠AOD+∠COD,即∠AOB=∠AOC，
∴∠BOM=∠COM.
由③知∠BOC=∠OCB，
又∵OM=OM.
∴△BOM≌△COM（AAS）.
第一章复习题第11题答案
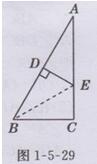
证明：如图1-5-29所示，连接BE.
∵DE垂直平分AB，
∴AE=BE.
∴∠ABE=∠A=30°.
∵∠C=90°，∠A=30°，
∴∠ABC=60°.
∴∠EBC=∠ABC-∠ABE=30°.
∴BE=2CE.
∴AE=2CE.
第一章复习题第12题答案
解：∠AED=∠C=90°, ∠B=60°，
∴∠A=30°.
∴AD=2DE=2.
∴AC=AD+CD=4.
∵∠A=∠A, ∠AED=∠C ,
∴△AED∽△ACB，
∴DE/BC=AE/AC ,
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
人教版八年级下册历史知识与能力训练答案
八年级下册地理阳光学业评价答案人教版
八年级下册历史新课程自主学习与测评答案人教版
八年级下册历史与社会思想品德课时特训答案人教版
八年级下册思想品德新编基础训练答案人教版
人教版八年级上册英语长江作业本答案
语文八年级上册学习与评价答案苏教版
人教版八年级上册英语作业本答案