第七章复习题第15题答案
解：一个四边形的4 内角中，能都是直角，不能都是锐角，最多有3个钝角.理由：若都是直角，则这个四边形是长方形；若都是锐角，则这个四边形的内角和不到360°，与四边形的内角和为360°矛盾；若钝角大于3个，则这个四边形的内角和大于360°，与四边形的内角和为360矛盾.
第七章复习题第16题答案
解：根据题意，得∠GEF=∠DEF=∠EFG=68°，
所以∠1=180°-∠GEF-∠DEF=44°，
因为AD∥BC,
所以∠1+∠2=180°，∠2=180°-∠1=180°-44°=136°.
第七章复习题第17题答案
解：由AB∥CD，得∠2=∠3，
所以∠1=∠2=∠3=∠4，
所以180°-∠1-∠2=180°-∠3-∠4，
再由内错角相等，两直线平行可得进入潜望镜的光线与离开潜望镜的光线是互相平行的.
第七章复习题第18题答案
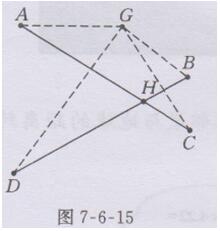
解：如图7-6-15所示，连接AC,BD，相交于点H，点H就是修建蓄水池的位置，取不同于点H的任意一点G，连接GA,GB,GC,GD，由三角形三边之间的关系，知：GA+GC＞AC,GB+GD＞BD,所以GA+ GB+ GC+GD＞AC+BD=HA+HB+HC+HD（若点G在AC或BD上（不与点H重合），同样可得GA+GB+GC+GD＞HA+HB+HC+HD）.
第七章复习题第19题答案
解：2∠A= ∠1+∠2.
理由：
在△ABC中，∠A+∠B+∠C=180°，
在△A’DE中，∠A’+∠A’DE+∠A’ED=180°，
又因为∠A=∠A’，
所以∠B+∠C=∠A’DE+∠A’ED.
在四边形BCDE中，∠B+∠C+∠1+∠2+ ∠A’DE+∠A’ED=360°，
所以∠1+∠2+2（180°-∠A’）=360°，即2∠A’=∠1+∠2，
所以2∠A=∠1+∠2.
第七章复习题第20题答案
解：（1）∠BOC=110°.点拨：∠BOC=90°+1/2∠A.
（2）∠B’O’C’=70°.点拨：∠B’O’C’=90°-1/2∠A’.
（3）由（1）与（2），得∠BOC与∠B’O’C’互补.同（1）可以求得∠OBC+∠OCB=1/2(180-n)°，∠BOC=180°-（∠OBC+∠OCB）=（90+1/2n）°；同（2）可以求得∠O’B’C’+∠O’C’B’=1/2(180-n)°, ∠B’O’C’=180°-(∠O’B’C’+∠O’C’B’)=( 90-1/2n)°.所以∠BOC+∠B’O’C’=180°.
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
七年级上册历史人教版长江全能学案答案
数学七年级下册学习与评价答案苏科版
人教版七年级上册生物知识与能力训练答案
七年级下册地理新课程自主学习与测评答案人教版
七年级下册地理同步导学与优化训练答案人教版
七年级下册数学书答案华东师大版
七年级下册地理同步训练答案人教版
数学七年级上册学习与评价答案苏科版