习题1.5第1题答案
解:∵AB∥CD,
∴∠BAD+∠ADC=180°,即∠BAE+∠EAD+∠ADE+∠CDE=180°.
∵∠BAE=25°,∠CDE=65°,
∴25°+∠EAD+∠ADE+65°=180°,
∴∠EAD+∠ADE=90°.
∴∠AED= 90°.
在Rt△AED中,由勾股定理,得AD2=AE2+DE2,
∴AD2=22+32=13,
∴AD=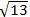 ,或AD=-
,或AD=-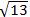 (舍去)
(舍去)
∴AD的长为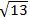 .
.
习题1.5第2题答案
解:如图1-2-32所示,
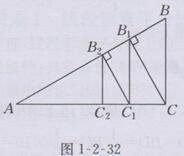
在Rt△ABC中,
∵∠A=30°,
∴BC=1/2AB=1/2×10=5(m)
在Rt△BB1C中,可得∠BCB1=30°,
∴BB1=1/2BC=1/2×5=2.5(m).
∴AB1=AB-BB1=10-2.5=7.5(m).
在Rt△AB1C1中,
∵∠A=30°,
∴B1C1=1/2AB1=1/2×7.5=3.75(m).
因此,BC的长为5 m,B1C1的长为3.75 m.
习题1.5第3题答案
解:假设树干与地面接触点为C . 由题意知△DEB为直角三角形 .
∵∠BDE=30°,
∴BD=2BE .
由勾股定理,得BE2+ED2=BD2=(2BE)2,
∴BE2+302=(4BE)2,解得BE=10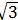 ≈17.32(m).
≈17.32(m).
∴ 树高BC=BE+EC≈17.32+1.52≈18.8(m).
因此,大叔的高度约为18.8m.
习题1.5第4题答案
解:没有,理由如下:
∵ 452+602=5 625≠4 900=702,
∴这个三角形不是直角三角形.
∴当60 m长的边线为南北向时,无东西向的边线.
习题1.5第5题答案
解:如图1-2-33(1)所示,将棱柱表面展开(部分),使A,B,A',B′,D′,C′在同一个平面内,根据勾股定理得
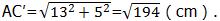
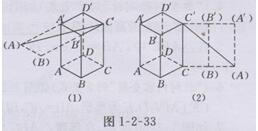
如图1-2-33(2)所示,将棱柱表面展开(部分),使A,A′,B,B′,C,C′在同一个平面内,根据勾股定理,得
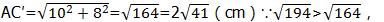
∴如图1-2-33(2)所示的展开形式中AC为最短路径.
因此,蚂蚁需要爬行的最短路径的长为2cm.

 苏科版八年级下册数学书答案
苏科版八年级下册数学书答案 北师大版八年级下册数学书答案
北师大版八年级下册数学书答案 八年级下册物理书答案北师大版
八年级下册物理书答案北师大版 译林牛津版八年级下册英语课本答案
译林牛津版八年级下册英语课本答案 苏教版八年级下册语文课本答案
苏教版八年级下册语文课本答案 人教版八年级下册英语课本答案
人教版八年级下册英语课本答案 北师大版八年级下册生物课本答案
北师大版八年级下册生物课本答案 北师大版八年级下册历史课本答案
北师大版八年级下册历史课本答案 浙教版八年级下册科学课本答案
浙教版八年级下册科学课本答案 人教版八年级下册生物课本答案
人教版八年级下册生物课本答案 人教版八年级下册数学作业本答案江西省
人教版八年级下册数学作业本答案江西省 人教版八年级上册历史新课程自主学习与测评答案
人教版八年级上册历史新课程自主学习与测评答案 人教版八年级上册英语作业本答案
人教版八年级上册英语作业本答案 八年级上册语文学法大视野答案人教版
八年级上册语文学法大视野答案人教版 北师大版八年级上册数学书答案
北师大版八年级上册数学书答案 八年级下册地理同步精练答案人教版
八年级下册地理同步精练答案人教版 语文八年级下册学习与评价答案苏教版
语文八年级下册学习与评价答案苏教版 八年级下册英语课时作业本答案人教版
八年级下册英语课时作业本答案人教版 人教版八年级上册数学课时练答案
人教版八年级上册数学课时练答案