习题1.3第1题答案
证明：
∵ AD∥BC(已知)，
∴∠1=∠B（两直线平行，同忙角相等），∠2 =∠C（两直线平行，内错角相等）
∵∠1=∠2（已知）.
∴∠B=∠C.
∴AB=AC（等角对等边）
习题1.3第2题答案
证明：
∵AB=AC，
∴∠B=∠C（等边对等角）
∵ EP⊥BC，∴∠B+∠BFP=90°，∠C十∠E=90°，
∴∠E=∠BFP.
∵∠BFP=∠EFA(对项角相等)，
∴∠E=∠EFA.∴AE=AF(等角对等边)，
∴△AEF是等腰三角形.
习题1.3第3题答案
(1)有两种情况：一种情况是锐角α为顶角，如图1-1-45所示（作法略），△A1B1C1为所求作的三角形；另一种情况是锐角α为底角，如图1-1-46所示（作法略），△A2 B2 C2为所求作的三角形.
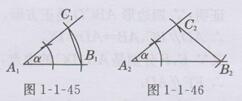
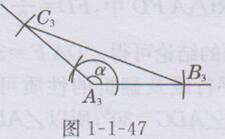
(2)因为底角只能为锐角，所以只有一种情况，即钝角α只能是顶角，如图1-1-47所示（作法略），△A3 B3 C3为所求作的三角形．
习题1.3第4题答案
解：∵∠NBC=∠C+∠NAC，∠NBC=84°，∠NAC= 42°，
∴∠C=∠NBC - ∠NAC=42°=∠NAC .
∴ AB= BC.
∴BC=18×10=180(n mile).
因此从B处到灯塔C的距离为180 n mile .
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册地理课时练答案人教版
人教版八年级下册语文知识与能力训练答案
浙教版八年级上册数学课时特训答案
八年级下册思想品德新编基础训练答案人教版
河北少儿版八年级上册生物作业本答案江西省
八年级下册物理同步导学与优化训练答案人教版
浙教版八年级上册数学作业本答案
人教版八年级上册语文作业本答案
八年级下册语文作业本答案人教版
人教版八年级上册物理作业本答案江西省