习题1.2第1题答案
解：设∠ABD=x°，
∵BD平分∠ABC，
∴∠ABC=2∠ABD=2x°.
∵AB=AC，
∴∠C=∠ABC=2x°.
∵BD=BC，
∴∠BDC=∠C=2x°，
∵∠BDC=∠ABD十∠A,
∴∠A=∠BDC-∠ABD=2x°-x°=x°.
∵∠A+∠ABC+∠C=180°，
∴x+2x+2x=180．解得x=36
∴∠A=36°.
习题1.2第2题答案
证明：
∵ AB=AC，
∴∠B=∠C
∵ AE=AF，
∴ AB-AE=AC-AF,即BE=CF.
∵D为BC的中点，
∴BD=CD.
在△BDE和△CDF中．
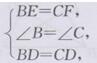
∴△BDE≌△CDF(SAS).
∴DE=DF(全等三角形的对应边相等)．
习题1.2第3题答案
证明：
∵△ABC是等边三角形，
∴∠A=∠BCE=60°，AC=CB
在△ACD和△CBE中，
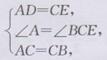
∴△ACD≌△CBE(SAS).
∴CD=BE（全等三角形的对应边相等）
习题1.2第4题答案
(1)证明：如图1-1-44所示，
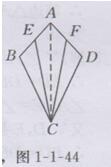
连接AC.在△ABC和△ADC中，
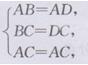
∴△ABC≌△ADC(SSS)，
∴∠BAC=∠DAC.
∵E、F分别为AB ,AD的中点，
∴AE=1/2AB，AF=1/2AD.
又∵AB=AD，
∴AE=AF.
在△AEC和△AFC中，
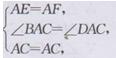
∴△AEC≌△AFC(SAS)，
∴EC =FC.
∴这两根彩线的长度相等.
(2)解：相等；相等；结论：只要AE=1/nAB，AF=1/nAD，就有EC= FC.
(3)解：如∠BEC=∠DFC或∠BCE=∠DCF等.
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册英语长江全能学案阅读训练答案人教版
人教版八年级下册物理南方新课堂答案
八年级下册物理长江作业本答案北师大版
八年级下册生物同步解析与测评答案人教版
八年级上册历史同步解析与测评答案人教版
八年级下册英语配套练习册答案人教版
八年级上册数学学法大视野答案华东师大版
人教版八年级下册历史知识与能力训练答案
八年级上册物理学法大视野答案人教版
人教版八年级下册语文知识与能力训练答案