习题7.2第1题答案
解：根据平行线的性质，由a∥b，得
①∠1=∠2，∠3=∠4，∠5=∠6，∠7=∠8.
理由：两直线平行，同位角相等.
②∠2=∠5=180°，
理由：两直线平行，同旁内角互补；
根据等量代换，两个叫互补的结论还有∠3+∠2=180°，∠3+∠8=180°等.
③∠2=∠7，∠4=∠5.
理由：两直线平行，内错角相等.
其他结论请自己尝试.
习题7.2第2题答案
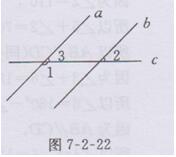
解：如图7-2-22所示，
因为a∥b，
所以∠3=∠2=45°（两直线平行，同位角相等），
所以∠1=180°-∠3=135°.
习题7.2第3题答案
解：画∠DCE=30°，CE交边AB于点E，则点即为所要找的点.
因为AB∥DC,
所以∠AEC+∠DCE=180°，
又因为∠DCE=30°，
所以∠AEC=180°-30°=150°，符合题意.
习题7.2第4题答案
解：相等的角有：∠DAC=∠ACB, ∠ADB=∠DBC, ∠AOD=∠BOC, ∠AOB=∠COD(O为AC与BD的交点).
理由如下：
因为AD∥BC，所以∠DAC=∠ACB，∠ADB=∠DBC（两直线平行，内错角相等）.
因为∠AOD与∠BOC，∠AOB与∠COD分别是对顶角，所以∠AOD=∠BOC，∠AOB=∠COD.
互补的角有：∠BAD与∠ABC, ∠ADC与∠DCB(不含邻补角).
理由如下：因为AD∥BC，所以∠BAD+∠ABC=180°，∠ADC+∠DCB=180°（两直线平行，同旁内角互补）.
习题7.2第5题答案
解：∠1=∠BAD.理由如下：
因为AD∥EF，所以∠2+∠BAD=180°（两直线平行，同旁内角互补）.
又因为∠1+∠2=180°，所以∠1=∠BAD（同角的补角相等）.
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
人教版七年级上册地理长江作业本答案
七年级下册思想品德课课练答案苏人版
人教版七年级上册数学作业本答案江西省
人教版七年级上册思想品德作业本答案
七年级下册历史同步导学与优化训练答案人教版
七年级下册地理同步精练答案人教版
七年级下册生物南方新课堂答案人教版
七年级上册数学人教版长江全能学案答案
七年级下册英语长江全能学案阅读训练答案人教版
七年级下册思想品德同步解析与测评答案人教版