习题1.1第1题答案
已知；已知；公共边；sss；全等三角形的对应角相等.
习题1.1第2题答案
证明：
∵BE=CF，
∴BE+EC=CF+EC，即BC=EF.
在△ABC和△DEF中，AB=DE，BC=EF，AC=DF,
∴△ABC≌△DEF(SSS)，
∴∠A=∠D（全等三角形的对应角相等）．
习题1.1第3题答案
解：∵AB=AC，
∴△ABC是等腰三角形.
∵AD⊥BC，
∴AD平分∠BAC.
∵∠BAC=108°，
∴∠BAD=1/2∠BAC=1/2×108°=54°.
习题1.1第4题答案
解：图中所有相等的角有：∠ABC=∠ACB，∠EBD=∠ECD．∠ABE=∠ACE，∠BAD =∠CAD．∠BED=∠CED，∠AEB=∠AEC．∠ADB=∠ADC.
理由：
∵AB=AC，
∴∠ABC=∠ACB（等边对等角）
∵AD_LBC，
∴∠ADB=∠ADC，∠BAD=∠CAD(等腰三角形的推论)
在△ABE和△ACE中，
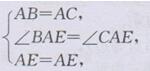
∴△ABE≌△ACE(SAS)
∴ ∠ABE=∠ACE. ∠AEB= ∠AEC（全等三角形的对应角相等）．BE=CE(全等三角形的对应边相等)，
∴∠EBC=∠ECB（等边对等角）
在等腰△BEC中，
∵ED⊥BC，
∴ED平分∠BEC(等腰三角形的推论)，即∠BED=∠CED.
习题1.1第5题答案
解：全等
已知：如图1-1-41所示，在△ABC和△A'B′C ′中，AB =AC．A ′B ′=A′C′，∠A=∠A'，BC=B ′C′，
求证：△ABC≌△A'B'C′.
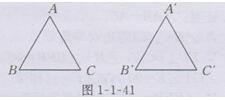
证明：
∵AB=AC，A'B'=A'C，
∴∠B=∠C，∠B′=∠C′（等边对等角）
∴∠B=∠C=1/2(180°-∠A)，∠B′=∠C′=1/2(180°-∠A′).
∴∠A=∠A′，
∴∠B=∠B′=∠C=∠C′
又∵BC=B′C′，
∴△ABC≌△A'B'C(ASA)
习题1.1第6题答案
解：BD=CE.
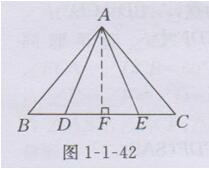
证明：如图1-1-42所示，过点A作AF⊥BC，垂足为F.
∵AB=AC．
∴AF是等腰△ABC底边BC上的中线，
∴ BF=CF
∵ AD=AE,
∴AF是等腰△ADE底边DE上的中线，
∴ DF=EF
∴BF-DF=CF-FF,即BD=CE.
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册历史与社会思想品德课时特训答案人教版
八年级下册地理课时练答案人教版
八年级下册物理长江全能学案同步练习册答案人教版
人教版八年级上册语文书答案
八年级下册科学作业本答案浙教版
数学八年级上册学习与评价答案苏科版
八年级下册物理同步导学与优化训练答案人教版
八年级下册历史长江全能学案同步练习册答案人教版
八年级下册历史新编基础训练答案北师大版
八年级上册数学同步解析与测评答案人教版